Provocarea de logica a saptamanii: Varza, Gogu si ceasurile (UPDATE cu rezolvarile)

O capră aduce acasă niște verze și pleacă la vânătoare. Iedul cel mic se trezește primul și mănâncă o șesime dintre verze. Următorul se trezește și mănâncă o cincime dintre verzele pe care le găsește în casă. Mijlociul se trezește și el și mănâncă un sfert dintre verzele care mai erau. Următorul se trezește și mănâncă o treime dintre verzele pe care le vede. În sfârșit, când se trezește, iedul cel mare mănâncă și el jumătate dintre verzele pe care le găsește. Când se întoarce de la vânătoare, capra găsește trei verze. Câte verze a adus acasă?

Gogu spune adevărul doar lunea, joia și sâmbăta. În toate celelalte zile minte. Într-o zi spune: „Mâine o să spun adevărul!” Ce zi e?

În sfârșit, pentru cei care vor o nucă mai tare am pregătit pentru astăzi, fiindcă tot se apropie vacanța, o problemă specială. Se spune că a fost dată la o olimpiadă de matematică în URSS. Motivul pentru care o propun aici este următorul: dincolo de rezolvarea matematică, există o rezolvare logică, în care nu avem nevoie de niciun calcul geometric. Problema sună așa: Avem 50 de ceasuri de mărimi diferite așezate pe o masă la întâmplare. (Asta înseamnă că unele pot fi cu ora 12 spre centrul mesei, altele cu ora 12 spre sud, altele cu ora 12 spre nord-vest ș.a.m.d.) Toate ceasurile funcționează și au fost potrivite la ora exactă. Ni se cere să demonstrăm că în decursul unei ore există un moment în care suma distanțelor dintre centrul mesei și centrul fiecărui ceas este mai mică decât suma distanțelor dintre centrul mesei și vârful minutarului fiecărui ceas.

Mențiuni

Din nou am avut o rundă fără câștigători de cărți, dar și o surpriză: cam jumătate dintre rezolvări au fost greșite. Bunăoară, mulți au considerat că „azi” din problema cu matematicienii de data trecută însemna „11 iunie”, chiar și după ce au apărut rezolvările. Sunt curios ce ar fi răspuns dacă problema ar fi fost propusă cu o săptămână înainte.

Le mulțumesc celor care au trimis răspunsuri și notări. Îmi cer scuze că nu le-am răspuns tuturor, dar au fost chiar foarte multe mesaje. Îi mulțumesc lui Mihai Negrea pentru verificarea problemelor.

NB: I-aș ruga pe cei care îmi trimit rezolvări prin e-mail să spună și cât de grea li se pare problema la care răspund (pe o scară de la 1 la 5). Mulțumesc. Comentariile, întrebările, propunerile, sugestiile și reclamațiile sunt așteptate la viorel.zaicu@hotnews.ro. Editura Paralela 45 sponsorizează gânditorii cu două titluri în fiecare săptămână: Boris Kordemski, 359 de probleme de matematică recreativă, și Martin Gardner, Cele mai îndrăgite jocuri matematice și logice. Premiile sunt oferite cititorilor care fie oferă o soluție originală (sau o explicație simplă și inedită) la problemele date, fie propun o problemă pe care n-am mai întâlnit-o (cel puțin nu în varianta respectivă). Nu vă străduiți să fiți originali cu orice preț – dacă sunt mai mulți câștigători o să fie și mai multe cărți!

Rezolvări

Capra

Problema e, totuși, o glumă. Calculul aritmetic e banal: 3 + 3 + 3 + 3 + 3 + 3 = 18 (A doua cifră este jumătate din suma primelor trei, a treia e o treime din suma primelor trei… iar a șasea e o șesime din suma totală.)

Gogu

Marți. Dacă ar fi una dintre zilele în care spune adevărul, în ziua următoare ar trebui să mintă (pentru că ar fi marți, vineri sau duminică, și ar minți), așa că este o zi în care minte. Dar minte că spune adevărul, deci o să mintă și a doua zi. Singurele zile consecutive în care minte sunt marți și miercuri, așa că ziua în care Gogu spune „Mâine o să spun adevărul!” nu poate fi decât marți.

Ceasurile

Rezolvarea matematică e ingenioasă și destul de complicată. Presupune construirea unui trapez dreptunghic variabil cu o bază dată de distanța dintre centrul mesei și centrul unui ceas și diagonala dată de distanța dintre centrul mesei și vârful minutarului unui ceas. (Ca în figura de mai jos.) Calculul raportului mediu dintre aceste două distanțe măsurate pe parcursul unei ore ne arată că diagonala medie este mai lungă decât baza medie luată în considerare. Rezultă astfel ceea ce ni se cere să arătăm.

FIGURA Ceas 1

Totuși, problema are și o soluție cu mai puține calcule. Dacă trasăm un cerc din centrul mesei până în centrul unui ceas oarecare, acesta va intersecta cercul trasat de vârful minutarului în două puncte, secționând astfel lungimea cercului în două. (Ca în figura de mai jos.)

FIGURA Ceas 3

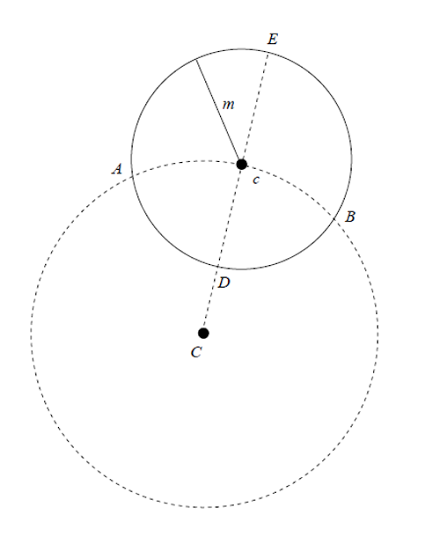
În punctele de intersecție A și B cele două distanțe pe care ni se cere să le comparăm sunt egale. De-a lungul unei ore distanța dintre vârful minutarului și centrul mesei (C) este mai mare decât cea dintre centrul mesei și centrul ceasului (c) pe un interval mai lung decât cel în care este mai mică, și anume cu atât mai lung cu cât lungimea minutarului este mai mare. De aici rezultă că, oricare ar fi orientarea ceasurilor, există cel puțin un moment de-a lungul unei ore în care suma distanțelor dintre centrul mesei și centrul fiecărui ceas (S1) este mai mică decât suma distanțelor dintre centrul mesei și vârful fiecărui minutar (S2). Puteți încerca să vedeți ce se întâmplă cu patru ceasuri care, dată fiind orientarea diferită, au la un anumit moment vârful minutarului în A, E, B și D, se află la aceeași distanță de centrul mesei și minutare de aceeași lungime. O să spuneți că sumele sunt egale. Ei bine, după un sfert de oră, douăzeci de minute sau douăzeci și cinci de minute diferența dintre cele două sume o să ne permită să spunem că s-a ajuns la o situație în care S1 este mai mică decât S2.

Putem să privim lucrurile și altfel, tot pe schema de mai sus: într-o oră, pentru un singur ceas media distanțelor dintre centrul mesei și vârful minutarului este mai mare decât distanța dintre centrul mesei și centrul ceasului (distanță pe care o putem considera medie). Asta nu înseamnă altceva decât că, dacă am lua în calcul 60 de ceasuri cu aceeași orientare care arată fiecare un minut al orei, S1 ar fi mai mică decât S2. (Mai mult, ar rămâne așa pe întregul parcurs al orei!) Excluzând cele mai mari 10 distanțe dintre centrul mesei și vârful minutarului, peste o jumătate de oră ar fi excluse cele mai mici 10 distanțe, deci am ajunge din nou la o situație în care S1 ar fi mai mică decât S2.

Nota redactiei:Comentariile la acest articol votr fi aprobate dupa publicarea rezolvarilor, duminica dimineata.

Cititi si provocarile de logica din saptamanile trecute:

Varstele copiilor si spargatorii

Caracatitele si propozitiile adevarate

Bacteriile si lantul

Sfertul de cerc si melcii strategi

Cartofii-minune si pastilele salvatoare

Guguta, ciorba si puntea afurisita

O cada de baie si 10 logicieni

Becuri si viteze

Bile, piulite si lacate

Apa si banii

Herr Casanova

Fitiluri si clepsidre

Inviorati-va neuronii cu problema lui Einstein

Provocarea de logica a saptamanii: Varza, Gogu si ceasurile (UPDATE cu rezolvarile)

MedLife, cea mai mare rețea de servicii medicale private din România, schimbă percepția românilor asupra spitalelor prin lansarea unei serii de evenimente culturale sub titlul: „Cultură și medicină: O alchimie a binelui”

#MediciBuni Dr. Ana-Maria Bota, medic primar ORL: „Tratez fiecare pacient așa cum m-aș trata pe mine însămi. Și mi se pare normal să fac asta”

#medicibuni Dr. Ioana Dumitrașcu-Biriș, medic cardiolog fetal MedLife: „Testele de ADN fetal nu pot înlocui ecografiile morfofetale în sarcină”

#medicibuni Dr. Horațiu Teodorescu, gastroenterolog MedLife: „Tusea, senzația de nod în gât și răgușeala ar trebui să aducă pacienții și la gastroenterolog“

#medicibuni Dr. Lucian Alecu, chirurg MedLife: „Dieta bazată pe alimente grase, procesate, pe consum de alcool și pe fructe dulci îmbolnăvește ficatul“

#MediciBuni – Dr. Ioana Raluca Sima: „ Cele mai multe dintre accidentele vasculare cerebrale și cazurile de demență pot fi prevenite”

#medicibuni Dr. Cătălin Magan, neurochirurg, despre o tânără cu fractură de coloană: „A ajuns la noi complet paralizată, am operat-o de urgență la MedLife Humanitas, iar acum a început să-și miște picioarele”

#medicibuni Dr. Tanita Mavriș, chirurg MedLife: „Adesea denumit «ucigașul tăcut», cancerul ovarian dă simptome precoce care pot fi confundate cu afecțiuni benigne”

MedLife prezintă tehnologia viitorului: de la drone și VR până la roboți medicali ce permit sigilarea vaselor direct de la consola chirurgului

MedLife achiziționează alți doi roboți da Vinci: „Este extraordinar că pacienții noștri vor avea acces la cea mai mare echipă de medici certificați în chirurgie robotică din România”

#medicibuni Dr. Cosmin Olariu, chirurg cardiovascular MedLife: „După 45 de ani, toți bărbații ar fi bine să fie văzuți de un cardiolog”

#medicibuni Dr. Laura Sinea, oncolog MedLife: „Cancerul mamar apare tot mai des la tinere, între 30 și 45 de ani. Este foarte important ca tratamentul să fie inițiat la timp”

#medicibuni Dr. Nicolae Florescu, cardiolog intervenționist MedLife, despre cele mai eficiente tratamente pentru afecțiunile severe ale inimii: „Am avut cazuri de mare risc, rezolvate cu bine, cu spitalizare redusă și cu evoluție ulterioară rapid favorabilă“

#medicibuni Dr. Victor Nimirceag, oncolog MedLife: „Pacientul vine deznădăjduit, cu un diagnostic greu, dar după discuția cu medicul, pleacă cu gândul că există soluții”

MedLife își consolidează poziția pe segmentul de oncologie printr-un nou parteneriat cu Institutul Sânului, extinzând serviciile dedicate tratamentului cancerului mamar

#medicibuni Dr. Cătălin Popa, chirurg MedLife: „Bărbații tineri sunt cei mai predispuși la hernia inghinală, mai ales dacă fac efort fizic într-un context nesusținut”

#medicibuni Dr. Cristian Țibea, ginecolog MedLife: „Avem o rată de succes foarte bună cu robotul, pentru că îmbină acuratețea operațiilor clasice, sau chiar mai mare, cu avantajele chirurgiei minim invazive“

După 14 diagnostice greșite, a ajuns la cel corect: un cancer urologic rar. Conf. dr. Florin Elec, urolog MedLife: „O intervenție chirurgicală cu tentativă de păstrare a rinichiului ar fi fost un dezastru pentru pacientă”

#medicibuni – Dr. Edina Iercan, medic dermatolog MedLife: „Persoanele active, care practică sporturi în aer liber, au nevoie regulat de screening dermatologic”

#medicibuni – Dr. Simina Condruz, oncolog MedLife: „Oncologia nu mai este o specialitate cu șanse mici de reușită. A progresat, avem multe terapii noi, iar pe pacient putem, de multe ori, să-l considerăm și vindecat”

#medicibuni – Dr. Claudiu Chitea, chirurg ortoped MedLife: „Sunt puține intervențiile ortopedice pe care să nu le putem face în România”

#medicibuni – Dr. Cristian Tefas, gastroenterolog MedLife : „Aproape 70% din totalul cazurilor de cancer colorectal ar putea fi prevenite dacă populația s-ar testa cu regularitate”

#medicibuni – Dr. Raluca Bidiga, pediatru MedLife: „Față de acum un deceniu, patologia pediatrică s-a schimbat. Au început să apară tot mai frecvent tiroiditele, diabetul, artritele”

Studiu MedLife: Tinerii români nu au nici informațiile, nici mijloacele necesare pentru a se proteja de bolile cu transmitere sexuală

#medicibuni – Dr. Denissa Olaru, oftalmolog la MedLife: „Lentilele de contact folosite incorect ne pun în pericol vederea și chiar ochii”

#medicibuni Dr. Diana Dobromir, medic-șef Laboratorul MedLife Medici’s: „Dacă nu sunt tratate, infecțiile cu Chlamydia și gonoreea pot duce la complicații severe”